We have seen a geometric proof and a classic algebraic proof for the sum of the geometric series, but there are many more. Here we point the reader to some of these proofs.
The first four deal with the finite geometric series, the rest with the infinite series. Does this suggest that the infinite case might be easier than the finite?
Euclid (Book IX Prop. 35 of the Elements) essentially uses the idea of telescoping series,
though in very unfamiliar garb, to find the sum of the finite geometric series,
by proving this equality of the ratio of the lengths:
( a rn - a ) / ( a + a r + a r2 + ... + a rn-1 )
= ( a r - a ) / a
Summing Geometric Series by Holding a Tournament, Vincent P. Schielack, Jr., The College Mathematics Journal, Vol. 23, No. 3 (May 1992), pp. 210-211.
Most of our students say this proof by Schielack is their favorite, perhaps because we often get to the section on geometric series at the height of March Madness! He considers a single elimination tournament and counts the number of games and the number of losers. The tournament idea only works for integer values of r, then one invokes uniqueness properties of polynomials to show it holds for all r.
Visualizing the Geometric Series, Albert Bennett, Mathematics Teacher, Vol. 82, No. 2, Feb 1989, pp. 130-136
This article uses areas of rectangles, an easy proof to follow though the construction works only for integer r.
The Geometric Series, Robert J. Clarke, The Mathematical Gazette, Vol. 81, No. 490 (mar 1997) pp. 92-93
Clarke applies the identity 1/(1-x) = 1/x + 1/x * 1/(1-x) recursively to obtain the finite geometric series.
The College Mathematics Journal, Vol. 29, No. 5 (Nov 1998), pp. 419-420.
An Investment Approach to Geometric Series, Robert Donaghey and Warren Gordon, The Two-Year College Mathematics Journal, Vol. 11 No. 2 (Mar 1980), pp. 120-121
Donaghey and Gordon use a perpetual annuity to motivate the formula for the sum of an infinite geometric series.
Proof without Words: Geometric Series, Sunday A. Ajose and Roger B. Nelsen, Mathematics Magazine, Vol. 67, No. 3 (Jun 1994), pg. 230
Our students like the pretty proof by Ajose which employs areas of squares and rectangles.
Geometric Progressions-A Geometric Approach, Michael Strizhevsky; Dmitry Kreslavskiy, The College Mathematics Journal, Vol. 32, No. 5 (Nov., 2001), pp. 359-362
This article relies on areas of triangles and gives a beautiful spiral visualization of the geometric series.
The Introduction to Infinite Series, W. J. Dobbs, The Mathematical Gazette, Vol. 9, No. 135 (May 1918) pp. 242-246
Infinite Series for Fifth-Formers, N. M. Gibbins, The Mathematical Gazette, Vol. 28, No. 282 (Dec., 1944), pp. 170-172
A Geometric View of the Geometric Series, Steven R. Lay, Mathematics Teacher, Vol. 78, No. 6, Sept. 1985, pp. 434-435
Proof Without Words: Geometric Series, the Viewpoints 2000 Group, Mathematics Magazine, Vol. 74, No. 4 (Oct 2001), pg. 320
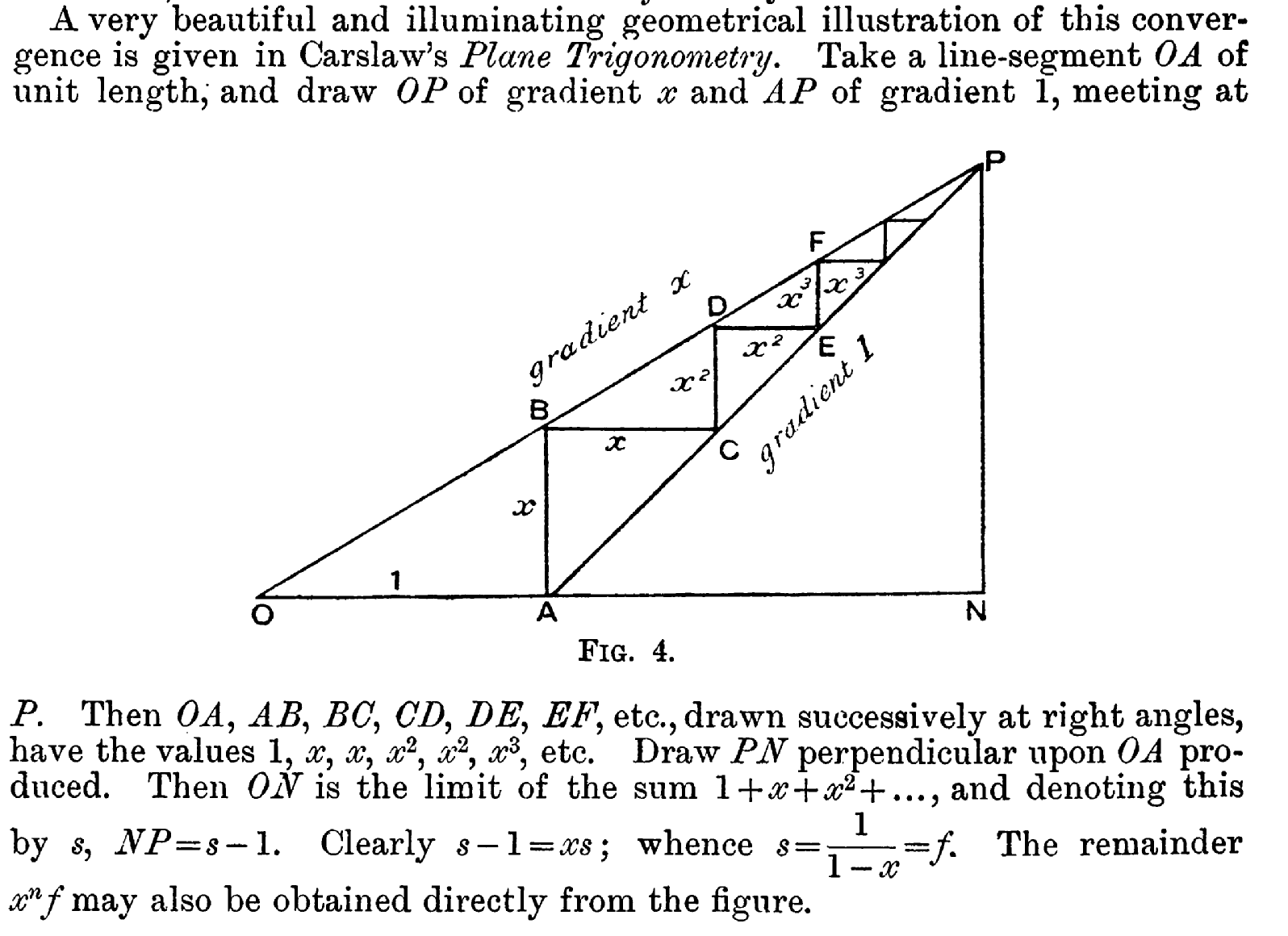
In 1918, Dobbs attributes to an earlier author a beautiful proof using fixed points of cobweb diagrams to show the sum of the infinite geometric series. Gibbins extends it slightly in 1944. In 1985 Lay rediscovered this proof, then the Viewpoints group rediscovered it again in 2000. Here is Figure 4 and the accompanying illustration from page 245 of Dobbs' article:
On a previous page we explicated the visual proof by Klein and Bivens which uses similar triangles. Other authors also use similar triangles to derive the sum of the infinite geometric series. Here is a list of some "similar triangle" proofs:
Proof without Words: Geometric Series, Elizabeth Markham, Mathematics Magazine, Vol. 66, No. 4 (Oct 1993), pg. 242
A Geometrical Construction for the Sum of a Geometrical Progression, F. J. W. Whipple, The Mathematical Gazette, Vol. 5, No. 81 (Oct., 1909), p. 139
The Geometric Series: A Geometric Demonstration, Michael Worboys, The Mathematical Gazette, Vol. 60, No. 413 (Oct 1976), pp. 204-205
A Geometrical Representation of the Sum of an Infinite Geometric Series, R. M. Milne, The Mathematical Gazette, Vol. 5, No. 81 (Oct 1909), pg. 138
A Diagram to Illustrate the Geometric Series, J. Gagan, The Mathematical Gazette, Vol. 38, No. 326 (Dec 1954), pg. 281
Convergence of Geometric Series, K. A. Deadman, The Mathematical Gazette, Vol. 54, No. 388 (May 1970), pp. 140-141
The wonderful 1993 MAA publication Proof without Words edited by Roger B. Nelsen contains more beautiful visual demonstrations:
In Proofs without Words, Roger B. Nelsen, Mathematical Association of America, 1993:
Warren Page: page 118, areas of squares and rectangles, also special case of r=1/2.
Webb, page 119, similar triangles.
Klein and Bivens, page 120, similar triangles.
Ajose, page 121, based on article referenced above, areas of squares and rectangles, also special case of r=1/4.
Markham, page 122, based on article referenced above, similar triangles..
Taken from: Nelsen, ed., Proofs without Words II, MAA , 2000:
Mabry, page 111, special case of r = 1/4 using areas of triangles.
Some other references on teaching geometric series:
Geometric Series on the Gridiron, Andris Niedra, The Two-Year College Mathematics Journal, Vol. 9, No. 1 (Jan., 1978), pp. 18-20
Geometric Series and the Rhind Papyrus, R. S. Williamson, The Journal of Egyptian Archaeology, Vol. 28 (Dec., 1942), p. 67
Note on the Convergency of the Geometric Series, W. H. H. Hudson, The Mathematical Gazette, Vol. 2, No. 27 (May, 1901), p. 60 (Note the date!)
Geometric Examples of Convergent Series, C. A. Barnhart, National Mathematics Magazine, Vol. 17, No. 4 (Jan., 1943), pp. 159-162
Next: The Final Answer: How Long does the Ball Bounce?
Previous: Geometric Series Part 2
copyright: Besson and Styer, Villanova University 12/22/2007
